Molassembler is a C++ library that aims to facilitate conversions between Cartesian and graph representations of molecules. It provides the necessary functionality to represent a molecule as a graph, modify it in graph space, and generate new coordinates from graphs. It can capture the absolute configuration of inorganic molecules with multidentate and haptic ligands from Cartesian coordinates and enumerate non-superposable stereopermutations at non-terminal atoms and non-isotropic bonds at arbitrary local shapes ranging up to the icosahedron and cuboctahedron.
This is the documentation for molassembler's C++ library.
This section aims to be a fast introduction to the concepts necessary to get productive with this library.
Molecule instances are composed of a Graph and a StereopermutatorList. The Graph represents atoms as vertices and bonds as edges in a mathematical graph. The StereopermutatorList is a container for stereopermutators, which are objects to handle the relative spatial arrangement of atoms. Atom stereopermutators are responsible for classifying the local shape of its substituents and allowing permutation through distinct non-rotationally superimposable arrangements of its substituents. One of the simpler stereogenic cases it manages is that of an asymmetric tetrahedron, where its two stereopermutations represent the R and S arrangements. Atom stereopermutators manage such arrangements in distinct shapes that range from two substituents (linear and bent) up to twelve (icosahedron and cuboctahedron). Bond stereopermutators are responsible for the relative arrangement of two atom stereopermutator instances fused at arbitrary vertices of their shapes. They manage, for instance, the E and Z arrangements at asymmetric double bonds.
Molassembler classifies the substituents around every non-terminal atom into a polyhedral shape if a Molecule is constructed with Cartesian coordinates.
In order to deal with haptic ligands, a further abstraction is introduced: Substituents are always grouped into binding sites made of contiguous sets of atoms. Then that set of atom's centroid is taken as a putative shape vertex position in shape classification.
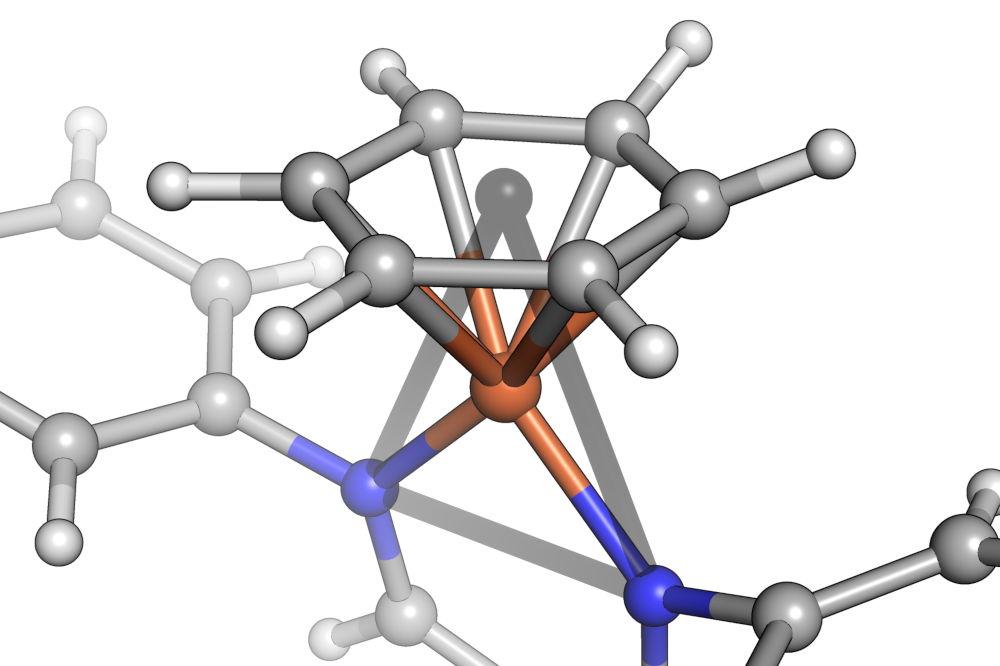
Alternatively, when molecules are constructed by a Graph only, this part of the construction is replaced by a shape inference algorithm that tries to guess reasonable shapes based only on graph information (which is limited in accuracy, generously speaking, as soon as inorganic centers are involved).
Now we need to figure out how many different non-superposable relative arrangements of the binding sites are possible within the classified shape. The operative word being different, the binding sites of each non-terminal atom are ranked according to extended IUPAC sequence rules. The ranking and links between sites are reduced to an abstract binding case such as \((A-A)_3\). From there, we enumerate the following non-superimposable cases within a particular shape, say, an octahedron:
Whether any of these stereopermutations are actually possible in a particular molecule depends on the length of the bridge between the binding atoms of the bidentate ligand. If it's very long, then perhaps all stereopermutations are possible. At intermediate lengths, the stereopermutations with trans-arrangements might be infeasible, and at very short bridge lengths (say, just one intermediate atom), none of them might be possible.
Molassembler takes the abstract enumerated stereopermutations and checks the feasibility of all bridges between any multidentate ligands, if present. Additionally, if there are haptic ligands, the cone it occupies is estimated and collisions between haptic ligands are avoided.
In a Molecule, atom stereopermutators are instantiated on each non-terminal atom. Atom stereopermutators store the local shape at this atom, all abstract stereopermutations (with relative statistical occurrence weights), the results of the feasibility checks, and which stereopermutation is currently realized. Note that terminal atoms aren't particularly interesting because their local shape has merely a single vertex and there isn't much to manage. The stereopermutation an atom stereopermutator is set as can only be determined if Cartesian coordinates are present. Otherwise, if there are multiple feasible stereopermutations but no way to determine which is realized, the atom stereopermutator is unspecified. This means that it represents all of its feasible stereopermutations. The conformational ensemble of a molecule with a single atom stereopermutator representing an unspecified asymmetric tetrahedron (where there are two possible stereopermutations, known by their stereodescriptors R and S), is essentially a racemic mixture.
Molassembler introduces a particular terminology here. Stereopermutators expose two different stereodescriptors. The first, the index of permutation, independent of any feasibility checks, is just a number ranging from zero to the number of stereopermutations minus one. From our example in an octahedron shape from before, there are four stereopermutations. The valid indices of permutation are then zero, one, two and three. Say within the particular Molecule, only the all-cis arranged stereopermutations are feasible. The set of feasible stereopermutations is indexed just like the set of all stereopermutations, and that index is called an assignment, because these are the only stereopermutations that you can assign a stereopermutator to. Assignments, like indices of permutations, are merely a number ranging from zero to the number of feasible stereopermutations minus one. In our octahedron example, there are two feasible stereopermutations, and valid assignments are zero and one.
Stereogenic arrangements of atoms due to rotational barriers around bonds are managed by bond stereopermutators. They can be formed with arbitrary assigned, adjacent atom stereopermutators. Like their atom-centric counterparts, a feasibility algorithm determines whether particular rotational arrangements are possible given any bridges connecting its ends. As a result, in carbocycles of sizes three to seven, bond stereopermutators composed of equatorial triangles, bent shapes or mixtures thereof are not stereogenic, i.e. only a single stereopermutation is feasible.
Keep in mind that bond stereopermutators are by no means connected with any sort of molecular orbital reasoning, and are purely phenomenological. Given a Molecule with any sort of flat cycle in its Cartesian coordinates, molassembler will instantiate bond stereopermutators on all edges of the cycle. Similarly, molassembler will not complain if a bond stereopermutator is instantiated on a bond of single bond order.
Now that we are familiar with the concepts of the molecular model, let us dive into some examples.
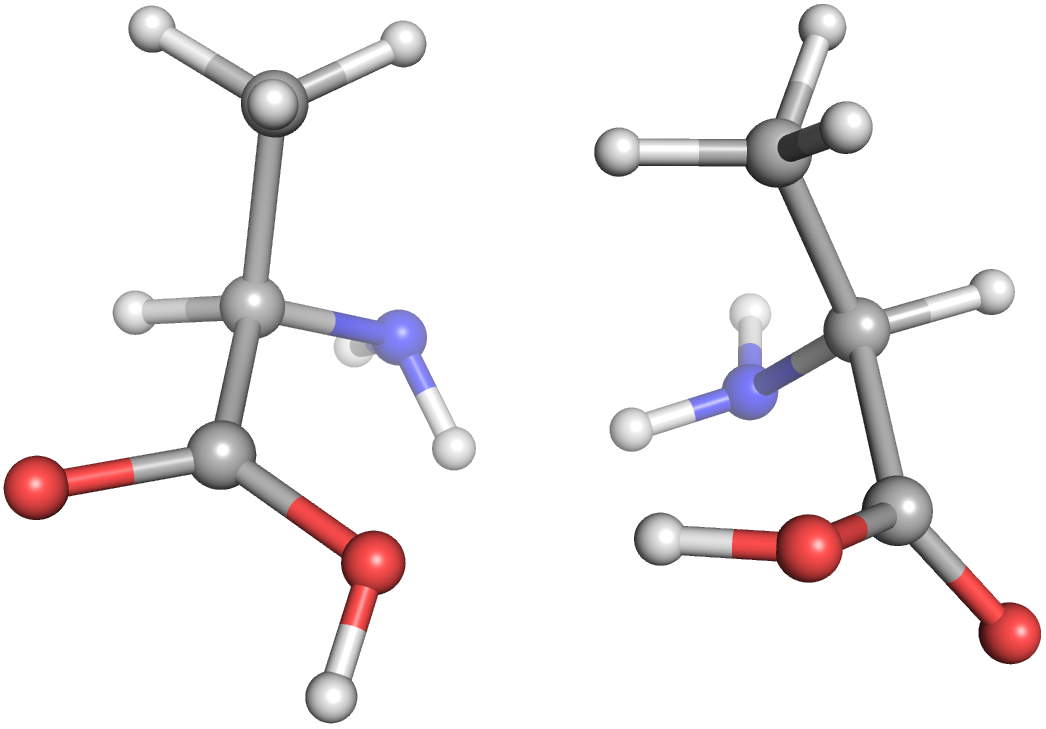
Let's get right into a Molecule example with multiple stereopermutations. Here, we're creating an alanine Molecule from a SMILES string, creating its enantiomer, generating a conformation for each molecule, and writing those to separate files.
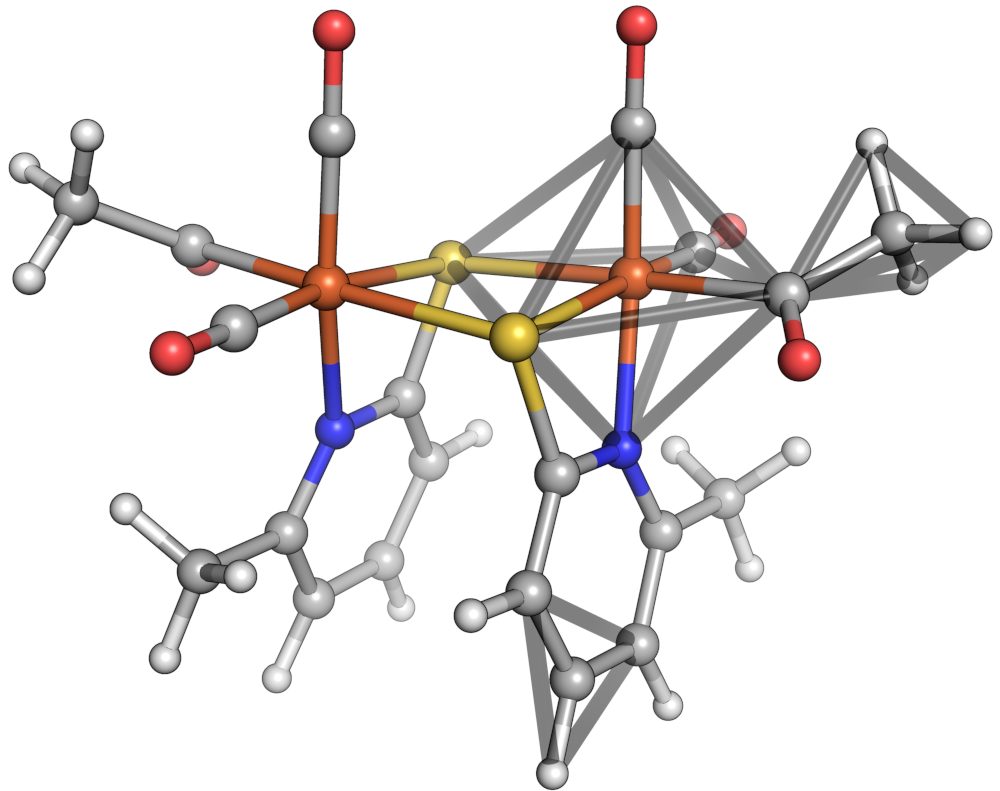
Let's move on to a multidentate complex in which feasibility is relevant. We'll consider the octahedral iron oxalate complex:
In the discretization of fractional bond orders to classic integer internal bond types (e.g. single, double, etc.), there are two options. You can choose to round bond orders to the nearest integer, but this is particularly error prone for particularly weakly-bound metal ligands (around 0.5) and aromatic bonds (around 1.5). For instance, two adjacent aromatic bonds that both show a fractional bond order around 1.5 may be randomly rounded up or down depending on the bond order generation method or its particular conformation. This can cause unexpected ranking inequivalency / equivalency artifacts. If you expect there to be conjugated systems or transition metals in your set of interpreted molecules, discretizing bond orders in this fashion is disadvised.
It is instead preferable to discretize bond orders in a purely binary manner, i.e. bond orders are interpreted as a single bond if the fractional bond order is is more than or equal to 0.5. Double bond stereocenters (i.e. in organic molecules E/Z stereocenters) are still interpreted from coordinate information despite the main bond type discretized to a single bond. This part of a Molecule's interpretation is discussed elsewhere.
If no coordinates are present when constructing a Molecule, the idealized shape on any non-terminal atom must be determined from its local substituents within the set of appropriately sized shapes. For main-group atoms, this is accomplished by application of a very basic valence shell electron pair repulsion (VSEPR) algorithm. No shape inference algorithms are currently implemented for non-main-group atoms, and the first shape of appropriate size is chosen instead.
In order to establish the relative priority of an atom's substituents, a ranking algorithm is applied that follows the IUPAC recommendations laid out in the 2013 Blue Book [4], generalized to larger shapes. The IUPAC sequence rules are as follows, slightly reworded:
| Nr. | Sequence rule |
|---|---|
| 1a | Higher atomic number precedes lower. Atomic numbers in Mancude rings and ring systems are the mean of the atomic numbers in all mesomeric Kekule structures. |
| 1b | A duplicate atom node whose corresponding nonduplicated atom node is closer to the root ranks higher than a duplicate atom node whose corresponding nonduplicated atom node is farther from the root |
| 2 | Higher atomic mass number precedes lower |
| 3 | When considering double bonds and planar tetraligand atoms Z precedes E and this precedes nonstereogenic double bonds. |
| 4a | Chiral stereogenic units precede pseudoasymmetric stereogenic units and these precede nonstereogenic units |
| 4b | When two ligands have different descriptor pairs, then the one with the first chosen like descriptor pairs has priority over the one with a corresponding unlike descriptor pair. Descriptors are alike if they are within the same set. The two sets are {R, M, Z} and {S, P, E}. |
| 4c | r precedes s and m precedes p |
| 5 | An atom or group with descriptors {R, M, Z} has priority over its enantiomorph {S, P, E} |
The following alterations arise due to the current implementation state:
In summary, the currently applied sequence rules are:
| Nr. | Sequence rule |
|---|---|
| 1a | Higher atomic number precedes lower. Atomic numbers in Mancude rings and ring systems are the mean of the atomic numbers in all mesomeric Kekule structures. |
| 1b | A duplicate atom node whose corresponding nonduplicated atom node is closer to the root ranks higher than a duplicate atom node whose corresponding nonduplicated atom node is farther from the root |
| 2 | Higher atomic mass number precedes lower |
| 3 | When considering double bonds and planar tetraligand atoms Z precedes E and this precedes nonstereogenic double bonds. |
| 4a | Chiral stereogenic units precede pseudoasymmetric stereogenic units and these precede nonstereogenic units |
| 4b | When two ligands have different descriptor pairs, then the one with the first chosen like descriptor pairs has priority over the one with a corresponding unlike descriptor pair. Descriptors are alike if they have an equal number of stereopermutations and equal index of permutation are within the same set. The two sets are {R, M, Z} and {S, P, E}. |
| 4c | r precedes s and m precedes p |
| 5 | An atom or group with higher index of permutation has priority descriptors {R, M, Z} has priority over its enantiomorph {S, P, E} |
Stereopermutation enumeration is accomplished similar to a method reported in the literature [1]. In particular, see the namespace Stereopermutations. Atom stereopermutations are enumerated by Stereopermutations::uniques. Bond stereopermutation enumeration is merely the rotational alignment of off-axis substituents (see Composite).
Point clouds are classified into polyhedral shapes by minimal continuous shape measure [8]. The algorithms for this are in the Shapes::Continuous namespace. An implementation of the suggested algorithm is given in shapeFaithfulPaperImplementation. There are several variations on this algorithm in this namespace, including variants with heuristics and fixed centroid mappings.
Cycle detection and enumeration is handled by the excellent library RingDecomposerLib [5] , which avoids exponential space requirements in heavily fused ring systems using Unique Ring Families [7] .
For each sought conformation, unassigned stereocenters in the input molecule are assigned randomly according to the relative statistical occurrence weights of the stereopermutations.
Conformer generation itself is based on four-dimensional Distance Geometry [2] . This library's implementation features the following:
Molecule instances can be canonicalized. Graph canonicalization is an algorithm that reduces all isomorphic forms of an input graph into a canonical form. After canonicalization, isomorphism tests are reduced to mere identity tests.
The canonicalization itself, however, is computationally at least as expensive as an isomorphism itself. Therefore, no expense is saved if an isomorphism test is to be computed only once for two molecules by canonizing both. Only if a molecule instance is to be a repeated candidate for isomorphism tests is there value in canonizing it.
This library takes the approach of adding a tag to molecules that identifies which components of the graph and stereocenters have been used in the generation of the canonical form. This tag is voided with the use of any non-const member function. Pay close attention to the documentation of comparison member functions and operators to ensure that you are making good use of the provided shortcuts.
It is important to note that canonicalization information is only retained across IO boundaries using JSON and the associated .masm or .json file suffixes.
The member functions provided are very modular. If you want the strictest definition of isomorphism, then the default arguments to canonicalize are correct, after which operator == defaults to an identity permutation check:
If, instead, you want to use a limited definition of equality, then you can specify fewer components of molecules for use in canonicalization or comparison:
Currently, this library models two types of stereocenters: The first models the atom-centric relative placement of substituents across geometries ranging from linear to square-antiprismatic. The second type models configurational permutations owing to bond-centric rotational barriers.
In order to determine whether a particular atom in a molecule is an atom-centric stereocenter, its substituents are ranked according to a nearly-compliant implementation of the IUPAC sequence rules as laid out in the 2013 Blue Book. The rankings are transformed into an abstract substituent case (e.g. octahedral (A-A)BBCD) and a symbolic computation is carried out to determine the number of permutations that are not superimposable via spatial rotations within the idealized shape. The set of resulting permutations of the substituent symbols is called the set of stereopermutations. If this set contains more than one stereopermutation, then the atom is an atom-centric stereocenter under that shape.
If substituents are haptic or multidentate, an additional algorithm removes stereopermutations it deems clearly impossible. All bridge lengths between pairs of chelating atoms of a multidentate ligand are checked against the atom pair's bite angle within the idealized shape. Additionally, haptic ligands' cones are checked to ensure they do not overlap. Indices within the set of not clearly impossible stereopermutations are called assignments.
Bond-centric stereocenters model rotational configurations of arbitrary combinations of two shapes and their respective fused shape positions. The fused shape positions of each side affect the overall permutations if the shape has multiple position groups. For instance, this is the case in square pyramidal shapes, where there are axial and equatorial shape positions.
In order to create a molecule instance, information can be supplied and inferred in many ways.
Minimally, the atoms' element types and their connectivity are needed to constitute a molecule's graph. From a graph, the presence of stereocenters can be inferred by using algorithms to determine the local shape at an atom using information present in the graph about its substituents. Any inferred stereocenters are unassigned, i.e. generated conformers will be composed of all possible stereopermutations at those stereocenters.
Atom connectivity can also be discretized from a bond order matrix, which in turn can be very roughly approximated using pairwise atom distances from spatial information.
Atom-centric shapes and its stereocenter assignments can be gleaned from spatial information.
Bond-centric stereocenters are interpreted at each bond where both ends have an assigned atom-centric stereocenter. If the supplied conformation matches a permutation of the bond-centric stereocenter, the bond-centric stereocenter is assigned and kept. Incidental matches and undesired dihedral freezes can be avoided by specifying a minimal bond order for which a rotational barrier can exist. Any bonds whose bond orders do not meet this threshold are not considered for bond-centric stereocenter interpretation.
Molecular file formats supply varying levels of information about molecules, ranging from the XYZ format, which supplies merely element types and spatial information, to the MOLFile format, which supplies element types, discretized connectivity and spatial information.
The global behavior of the library can be altered in several respects.
In some cases, whether an atom is a stereocenter is dependent on ambient temperature. Trigonal-pyramidal nitrogen can invert rapidly at room temperature, but is a stereocenter at low temperature. By default, the library invokes the high-temperature approximation, where trigonal-pyramidal nitrogen centers can only be a stereocenter if it is part of a small cycle (sizes 3, 4) where the strain hinders inversion.
While editing a molecule on the graph level, the library attempts to propagate existing chiral state in its list of stereocenters to the new graph. By default, state is propagated only if a singular mapping of indices to the new shape exists in which no shape angles are altered. Which propagations of chiral state are acceptable can be altered.
The pseudo-random number generator is centralized and can be re-seeded for reproducible behavior.
The maxim of the library is to permit the specification of any desired graph, however unreasonable, within the logical constraints of the molecular model. These constraints are that a Molecule class can only contain a single connected component and must consist of at least one atom. Apart from that, you can create completely unreasonable graphs. Keep in mind, however, that these can be at odds with either the reduction of stereopermutations to assignments, where algorithms throw out obviously impossible permutations (yielding stereocenters with no possible assignments) or with the library's spatial modeling in conformer generation.
Information about a Molecule can be obtained from its constituting graph and stereocenter list classes, but editing is centralized at the Molecule interface since graph and stereocenter changes force a full re-ranking of all atoms and possibly changes in the list of stereocenters.
Among the possible changes in the list of stereocenters on re-ranking are:
It is therefore important that upon each molecular edit, any state about or within the StereopermutatorList of the molecule being edit that is stored externally to the instance itself is considered invalidated.
On a graph level, each constituting atom of a haptic ligand that is part of the bond of the ligand to a transition metal must have a bond to that transition metal. These bonds are of the Eta bond type, regardless of their individual order. It is, however, the task of the library to differentiate which bonds between atoms are to be considered an Eta bond type and which are not, based wholly upon the graph structure. The public API of molassembler does not accept user-defined Eta bond types. Specify Single as bond type in the creation of haptic bonding.
The generation of conformational ensembles of molecular graphs has a few peculiarities you need to know about.
It is very explicit in the library that conformer generation can fail. The possibility of failure is expressed by the explicit result type of conformer generation interfaces, which is essentially a two-state variant type holding either your requested conformational ensemble or some information about the reason for failure. The possibility of failure is explicit precisely to force you to consider it when integrating this library. A molecule you have generated may have stereopermutators with no possible assignments due to too short bridge lengths for multidentate ligands or too many large haptic ligands whose cones overlap in all arrangements. It may also conflict with the spatial model, which has upper limits on granted slack for particularly strained graphs.
All headers in the top-level library directory of molassembler and files included from there form the public interface. None of the files in deeper directories are part of the public interface and should be depended upon. Even the sub-libraries Temple, Shapes and Stereopermutation should be considered unstable, although they contain types that make up the public interface such as Shapes::Shape.
The top-level headers can be considered stable and future releases will do their best to maintain their stability. No guarantees are made regarding ABI stability and it is disadvised to relink without recompiling.
In general, API types follow the private implementation pattern and do not expose implementation types. All top-level include headers comprise the library API and have shallow include dependency trees. Types and functions exposed in these headers are intended for consumers.
MASM_NO_EXPORT, carry an explicit warning that they exist solely for library-internal purposes, and typically yield incomplete types. It is advisable not to use these functions or create functionality dependent on possibly forward-declared types involved. They do not form part of the public interface and are thus subject to free developmental flux.